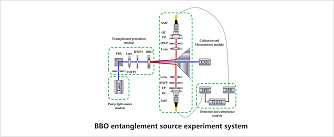
WT-ESS-BBO - установка для изучения явления квантовой запутанности
- Генерация и детектирование пар запутанных фотонов.
- Спонтанное параметрическое преобразование с понижением частоты (SPDC).
- Эксперимент по измерению значения параметра Бэлла.
- Эффект квантового "ластика".
Установка для изучения явления квантовой запутанности
Эта система основана на параметрическом процессе преобразования в кристалле BBO(β-Барий-Борат) с понижением частоты. Световой пучок лазера накачки падает на кристалл параметрического преобразования и при условии синхронности фаз генерируется поляризационно-сопряженные запутанная пара фотонов. Благодаря системе высокоточного позиционирования положения пространственного коллиматора можно с легкостью направить сгенерированную пару запутанных фотонов в волокно. Другой конец волокна подключается к однофотонному детектору, который преобразует свет в электрические импульсы. Электрический импульс отправляется на счетчик зарегистрированных фотонов, и выводится на его экране для реализации измерений параметров запутанности.
Спонтанное параметрическое преобразование с понижением частоты
Спонтанное параметрическое преобразование с понижением частоты (SPDC) использует нелинейный эффект второго порядка нелинейных оптических кристаллов. После того как свет накачки с частотой ωp проходит через нелинейно-оптическую среду, генерируются два запутанных фотона с частотами ωs и ωi , которые обычно называют сигнальным (signal) и холостым (Idler) соответственно.
ωp = ωs + ωi (1)
kp = ks + ki (2)
Описанный выше процесс сохранения импульса называется фазовым синхронизмом. Эффективность параметрического преобразования сильно зависит от степени фазового синхронизма. Процесс, при котором генерируется два фотона одинаковой частоты (ω s = ω i) называется удвоением частоты или процессом гармоники второго порядка.
В случае коллинеарного умножения частоты условие фазового синхронизма можно записать в виде скалярного выражения: k 2 ω =2 k ω . Так как k =nω / c , то n2·(2ω) · 2ω / c = 2n1(ω) · ω / c , и тогда n2(2ω ) = n1(ω). В видимом и ближнем инфракрасном диапазонах большинство нелинейно-оптических кристаллов обладают нормальными дисперсионными свойствами, т. е. n2(2ω) > n1(ω), и условие фазового синхронизма не может быть выполнено.
В экспериментах фазовый синхронизм часто достигается за счет двулучепреломления кристаллов. Для одноосных и двуосных кристаллов, в отличии от трехосных кубических, оптические свойства анизотропны, то есть показатель преломления света с разными состояниями поляризации различен при прохождении через кристалл, поэтому мы можем использовать характеристики двулучепреломляющего кристалла для компенсации разницы коэффициентов преломления. Дисперсионная характеристика кристалла заставляет фотоны основной частоты и сгенерированные фотоны двойной частоты с различными поляризациями удовлетворять условию n2(2ω) = n1(ω), чтобы достичь фазового согласования.
В качестве примера на рис. 1 показаны слои показателя преломления света основной частоты (сплошная линия) и света двойной частоты (пунктирная линия) одноосного кристалла BBO ( no > ne ). Как показано на рисунке, поверхности показателей преломления ne(2ω) и no(ω) пересекаются. Показателя преломления равны, что удовлетворяет условию фазового синхронизма. Направление вектора от центральной точки O до точки пересечения M является направлением фазового синхронизма, а угол Φ между оптической осью и OM является углом фазового синхронизма. Любое сагиттальное направление на конической поверхности кристалла, образованной вращением вокруг оптической оси с ОМ в качестве образующей, также может удовлетворять условию фазового синхронизма.
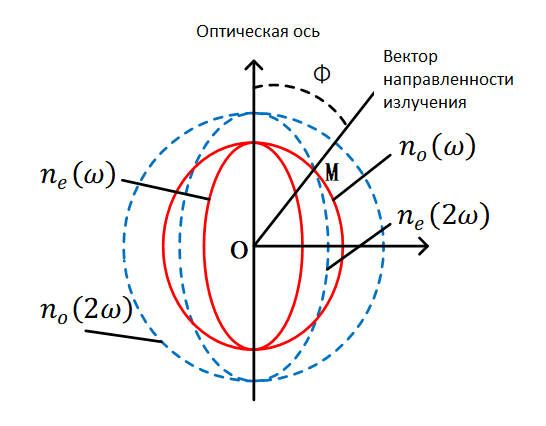
Рис. 1 Поверхностная диаграмма показателя преломления отрицательного одноосного кристалла
Эксперимент по измерению значения параметра Бэлла.
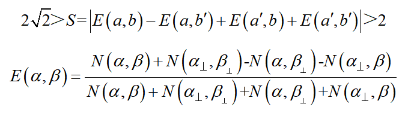
При генерации двух запутанных фотонов светом накачки, один из фотонов называется сигнальным, а другой холостым. В неравенстве Белла α представляет собой угол поворота поляризации сигнального фотона, а β представляет собой угол поворота поляризации холостого фотона. Среди них α =-45° , α⊥ = 45° , α′ =0° , α′⊥ = 90° , β = -22,5° , β⊥ =67,5° , β′ =22,5° , β′⊥ = 112,5o. N ( α , β ) представляют количество совпадений двух путей.
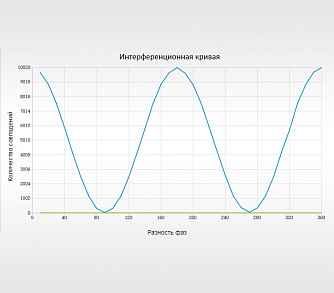
При измерении данных нам сначала нужно получить относительное положение 0°, потому что указанные выше параметры являются относительными углами поляризаторов. Теоретически, когда относительный угол между ними равен 0°, количество совпадений в это время имеет максимальное значение.
Эксперимент по калибровке угла наклона волновой пластины
| Комплектующие | Описание | Кол-во. |
|---|---|---|
| Лазер | Длина волны излучения 808 нм | 1 |
| Коллиматор |
Рабочая длина волны 780 нм, Фокусное расстояние 8 мм |
1 |
| Четырехосевой позиционер |
Оптический ход (XY) ±2 см, Диапазон углового позиционирования ±4° |
1 |
| Поляризационный делитель луча |
Рабочая длина волны 810 нм, Коэффициент экстинкции >1000:1 |
1 |
| Поляризатор |
Рабочая длина волны 810 нм, коэффициент экстинкции >500:1 |
2 |
| Полуволновая пластинка |
Рабочая длина волны 810 нм, Истинный нулевой порядок пластины |
4 |
| Пластина λ/4 |
Рабочая длина волны 810 нм, Истинный нулевой порядок пластины |
2 |
| Измеритель оптической мощности | Диапазон длин волн 300 - 1100 нм | 1 |
Набор для эксперимента по конфигурации и генерации пары запутанных фотонов
| Комплектующие | Описание | Кол-во. |
|---|---|---|
| Источник излучения | Длина волны излучения 650 нм | 1 |
| Многомодовое волокно | Диаметр 62,5/125 мкм | 2 |
| Коллиматор |
Рабочая длина волны 780 нм, Фокусное расстояние 8 мм |
4 |
| Четырехосевой позиционер |
Оптический ход (XY) ±2 см, Диапазон углового позиционирования ±4° |
2 |
| Оптический держатель | Диаметр 25,4 мм | 2 |
Набор для измерения параметра Бэлла
| Комплектующие | Описание | Кол-во. |
|---|---|---|
| Модуль генерации запутанных фотонов |
Длина волны накачки 404,6 нм, Максимальная мощность 40 мВт |
1 |
| Модуль тестирования источника запутанных фотонов | Длина волны 810 нм | 2 |
| Детектор одиночных фотонов | Модель SPCM-AQRH-12 | 2 |
| Счетчик совпадений | Модель WT-CC302 | 1 |
| Источник питания постоянного тока |
Диапазон напряжения 0 - 30 В, Три канала |
1 |
- Научные исследования в области квантовой механики и оптики.
- Измерение значения Бэлла.
- Генерация и детектирование пары запутанных фотонов.